Parallel Alpha-Beta Pruning of Game Decision Trees:
A Chess Implementation
Kevin Steele
CS 584 Fall 1999 Semester Project Report
Abstract
Computer chess has been actively researched since the 1970’s and has seen many advances in evaluation heuristics, internal representation, and especially tree search techniques. Since parallel supercomputers represent both historic and current participants in computer chess, a number of parallel tree-searching techniques have been developed to bring parallel technology advantages to the chessboard. For my semester project I implemented a parallel chess program using an established parallel search algorithm, principle variation splitting. I used two methods to divide tree nodes among parallel processors, even splitting and master/slave, and analyzed search times for both methods. The master/slave approach far outperformed the even splitting method, searching a 4-ply tree with 16 processors in about 5 seconds.
Introduction
Computer chess has been an area of interest in artificial intelligence research for nearly two decades. Researchers sought to mimic human intelligence by developing chess-playing algorithms for computers. Since then computer chess has carved its own niche in the computing world; computer chess conferences and tournaments are regular events [11], specialized hardware is developed for ultimate speed, and better algorithms, especially in the realm of parallel computing, are a topic of ongoing research.
Chess-playing programs use a data structure common to game theory—the game decision tree. Game decision trees are perfectly balanced fixed-depth trees whose search space is typically very large. For example, an average board position in the middle game of chess might have an average of between 35 and 38 possible moves. If a particular chess match has 50 moves for each color, the decision tree for the match has on the order of 35100 leaf nodes. Search algorithms for decision trees usually only search to a fixed depth bounded by time, accuracy, or other criteria.
A popular method for bounding the search space on decision trees is alpha-beta pruning [4]. This algorithm permits a much deeper decent into the search space by pruning away much of the tree as the search progresses. Alpha-beta pruning combined with iterative deepening of the search space provides a powerful mechanism for examining a useful chunk of the decision tree in an acceptable amount of time.
Serial computer chess is well developed and has historically proven its prowess. It is logical, however, to desire to outperform the serial algorithms by using parallel computer architectures. To investigate the capabilities of parallel alpha-beta pruning algorithms, I implemented a parallel chess program, pChess, using a parallel search tree algorithm. I tried two minor variations of the algorithm and contrasted the results.
Chess Program Implementation
My implementation of a computer chess program was done in C++, though no classes were used. The major components of the program included a data structure to represent the game state, a function to generate possible moves from a given board position, and an evaluation function to give an explicit score to a board position. Each of these components is described in detail.
The game state data structure contains the contents of all 64 squares on the chessboard as well as the locations and states of all 32 pieces. Using separate data structures for the board and pieces allowed more optimized move generation and score evaluation. There is an additional variable containing information such as which color is to move, castling status, etc.
The move generator computes the standard moves for each type of piece and includes castling, pawn promotion, and capturing en-passant. A unique index is used for each possible move of each piece type. Indices for moves along the principle variation are saved in an array for use in iterative deepening. A fairly modest opening book containing four variations of P-K4 is used during the opening game—center game, Danish gambit, king’s gambit, and king’s gambit declined.
The evaluation function awards points for various captures and board positions. Points are added for the capture of pieces, control of the center, castling, pawn advancement, protection, and promotion, checking the opponent, and checkmating. Points are subtracted for losing the chance to castle and doubling pawns. At each evaluation, the function is called for each side, and the overall score is the difference between the two individual scores. The appropriate sign is applied depending on whether the search is finding minimums or maximums.
The program has several playing modes: computer vs. itself, computer vs. user, or user vs. user, though the last mode was never utilized. Playing the computer vs. itself mode was useful for playing batches of games and compiling the results for timing analyses. Playing the computer vs. user mode was useful for debugging and for playing my program against a computer chess game.
Several chess rules and optional items were not implemented in my program due to time constraints. The 50-move stalemate rule was not implemented, though it is accounted for in the evaluation function. The 3-repeated move stalemate rule was not implemented. Promoted pawns can only be promoted to queens, and my program recognizes only four promoted pawns per side as being queens. Additionally, most computer chess programs implement two enhancements that greatly improve speed and accuracy, neither of which I included in my program. The first is the use of transposition tables, which records recently evaluated positions in a hash table. This eliminates much of the overhead incurred by repeated searches during iterative deepening. The second is quiescence searching, which is performed at the leaf nodes of the full search. Quiescence searching continues the search deeper in the tree by only playing out capture moves and pawn promotions, simulating the way humans play out tactical exchanges in their minds. The evaluation function is then applied at the new leaf nodes to score the tactically quiet board position, resulting in a more accurate score for a given move.
Alpha-Beta Pruning
The most efficient method to traverse a minimax game tree is the alpha-beta pruning algorithm. This algorithm effectively prunes portions of the search tree whose leaf node scores are known a priori to be inferior to the scores of leaf nodes already visited. Knuth [4] showed that alpha-beta pruning can reduce the number of leaf nodes visited in a perfectly ordered tree of depth d with w possible successor branches at each node from wd to w[d/2] + w[d/2] – 1. Though many variations of alpha-beta pruning have evolved over time for computer chess, such as NegaMax, NegaScout, and aspiration search [7, 9], are all based on the fundamental principle of comparing scores against a minimum/maximum window.
Parallel Alpha-Beta Pruning
Unfortunately for parallel computing enthusiasts, the alpha-beta algorithm and its variations are inherently sequential. In fact, if great care is not given in parallelizing the algorithm, parallel performance can degrade well below the performance of the serial algorithm [2]!
A number of parallel versions of the alpha-beta pruning algorithm [1, 3, 5, 8] have been developed with varying degrees of success. I chose the principle variation splitting algorithm [5] because of its simplicity of design, ease of implementation, and its relatively good performance. Principle variation splitting parallelizes recursively along alpha-beta type 1 nodes [4], beginning at the lowest point in the tree. A number of alternatives are available in choosing how to divide branches of a node among processors. I implemented two approaches, evenly splitting the children and using a master/slave model, and compared the results. I used the MPI library to effect communication and synchronization.
The tree search implementation uses iterative deepening; it searches to depth one, then restarts the search to depth two, then restarts to depth three, etc. The path of the best score, the principle variation, is kept after each search iteration. At each iteration and at each depth in the search tree, the principle variation is searched first to establish the best possible minimum/maximum bounds from the previous search. Then the remaining moves at that tree depth are searched.
I used two methods, or models, to divide up n children of alpha-beta type 1 nodes among p parallel processors. The first method, the even split model, gives each available processor n/p nodes to process independently. After all processors have completed their subtree searches, MPI_GATHER is used to bring all the processor’s best search results to processor 0. That processor then finds the globally best score and path and broadcasts them to the other processors. The search then continues higher in the tree.
The second method, the master/slave model, uses processor 0 as a master to relegate workloads to the other slave processors. When a slave processor is ready for work, it sends a work request to the master, which in turn gives the slave either a subtree to search or a stop message when no more work is to be accomplished at that tree depth. Upon completing the subtree search, the slave sends the results back to the master, which compares them to previously accumulated results. When all subtrees of a type 1 node of a given depth have been searched, the resulting best score and path are broadcast to all processors, and the search continues higher in the tree.
Results
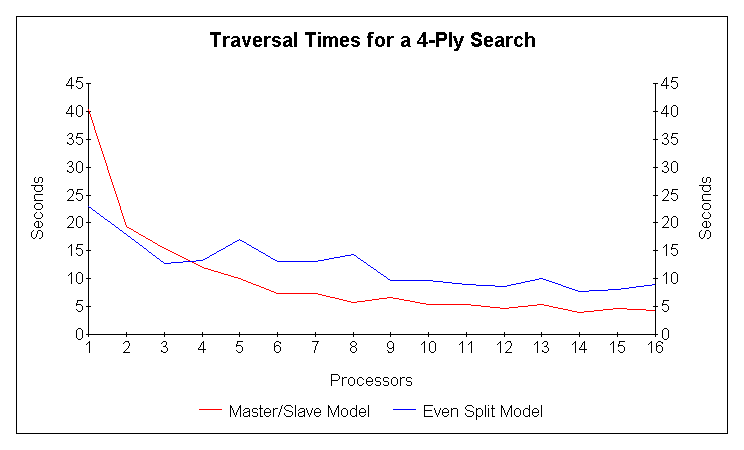
To compare and contrast the performance of the two models, I used my chess program implementation in computer vs. itself mode to play a number of games using each model. The game trees were searched to 4 ply, or four moves ahead, and search times were tallied and averaged for each move. To expedite the gathering of results, the computer played out only the first 20 moves of each game, roughly half the length of an average game. This put the computer well into the middle game of each game, where moves took the longest to compute, so the times were fairly well represented. Figure 1 shows the performance times for the two models.

Figure 1:
Traversal times for a 4-ply (depth 4) search.The even split model performed better for up to three processors, but when using four or more processors, the master/slave model performed better. Performance for both processors leveled out after about six processors. Figure 2 shows the speedups for the two models.
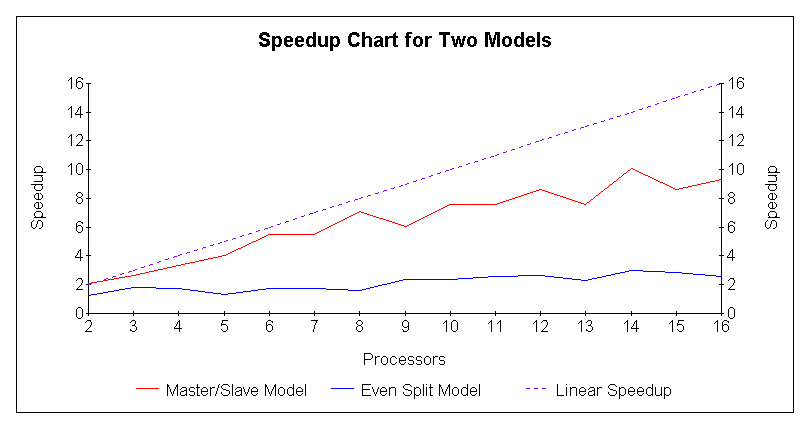
Figure 2:
Relative speedup of the two models.The even split model showed little speedup, whereas the master/slave model showed acceptable, much closer to linear, speedup. Figure 3 shows the efficiencies of the two models.
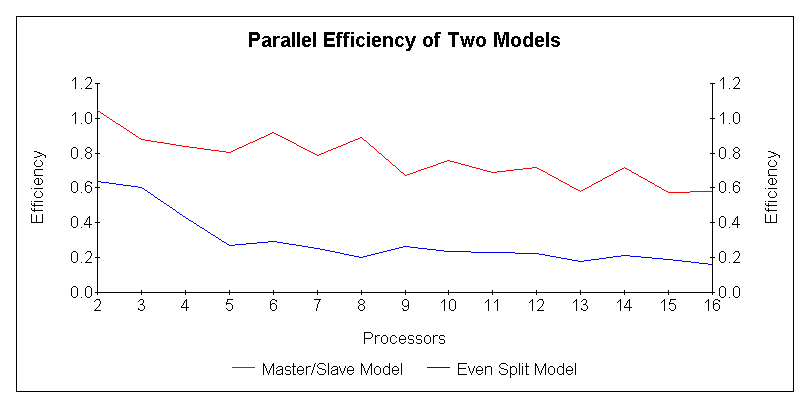
Figure 3:
Efficiency of the two models.As expected from the speedup graphs, the master/slave model was more than twice as efficient in its use of parallelism. It exhibited a bit of super-linear speedup when going from one to two processors, due to the unnecessary communication overhead present when using only one processor.
Why was the master/slave model so much more efficient than the even split model? For two simple reasons: most subtrees of type 1 nodes are trivial, and of the remaining subtrees, some are up to two orders of magnitude more complex than others. Evenly splitting subtrees among processors means that most processors sit idle most of the time while only a few processors do most of the searching, yielding low efficiency. The master/slave model permits all processors to continue working until all subtrees have been assigned. This yields higher efficiency and hence lower search times.
However, I observed that while the master/slave model sped up searching considerably, it still suffered from having idle processors. Apparently, when a move is found with a more favorable score than the principle variation obtained on a smaller depth search, the processor searching that subtree takes much longer to complete its search than all other processors. Since no more subtrees remain to be searched, the remaining processors wait until the most complex branch is completed. One obvious solution would be to first identify the most complex branch, then deploy all idle processors to assist in the searching that branch.
To show that my program could actually play a full game and checkmate an opponent, I played it in computer vs. user mode using 16 processors in the master/slave search model against a Tandy® 1650 portable computerized chess game. My program beat the Tandy computer in every game on its first level, but only won about 20% of the games on its second level; I didn’t bother playing it on higher levels. This merely showed that at the higher skill level the Tandy computer searched deeper in the decision tree than my program. However, the Tandy computer was also much slower in making its moves than my 16 node cluster, illustrating that parallel algorithms can at times outperform serial algorithms running on specialized hardware.
Conclusion
The results suggest that parallel implementations of alpha-beta pruning can add considerable performance to computer chess programs. This is evident in the renowned rematch of Kasparov vs. IBM’s Deep Blue chess system, in which the computer defeated the current world champion Garry Kasparov 3.5 to 2.5 [6]. "Deep Blue is at heart a massively parallel, RS/6000 SP-based computer system that was designed to play chess at the grandmaster level." [10]
Parallel alpha-beta pruning algorithms still have problems, however, and the evidence of continued research suggests that the best solutions have not yet been found.
References
[1] Bal, H.E. and Renesse, R. van, A Summary of Parallel Alpha-Beta Search Results. ICCA Journal, 9(3):146-149, 1986.
[2] Fox, G.C., Williams, R.D, Messina, P.C, Parallel Computing Works. Morgan Kaufmann Publishers, 1994.
[3] Hyatt, R.M., Suter, B.W. and Nelson, H.L. A Parallel Alpha/Beta Tree Searching Algorithm. Parallel Computing, 10(3):299-308, 1989.
[4] Knuth, D. E., and Moore, R. W. An Analysis of Alpha-Beta Pruning. Artificial Intelligence, 6:293-326, 1975.
[5] Marsland, T.A. and Popowich, F., Parallel Game Tree Search. IEEE Transactions on Pattern Analysis and Machine Intelligence, 7:442-452, 1985.
[6] Pandolfini, B., Kasparov and Deep Blue: the historic chess match between man and machine. Simon and Schuster, New York, 1997.
[7] Reinefeld, A. An Improvement to the Scout Tree-Search Algorithm. ICCA Journal, 6(4):4-14, 1983.
[8] Schaeffer, J. Improved Parallel Alpha-Beta Search. in H. Stone and S. Winkler, editors, Proceedings of ACM-IEEE Fall Joint Computer Conference, pages 519-527. ACM Press, New York, NY, 1986.
[9] Weill, J.-C. The NegaC* Search. ICCA Journal, 15(1):3-7, 1992.
[10] http://www.research.ibm.com/deepblue/learn/html/e.html; Learn About the Technology.
[11] http://www.uni-paderborn.de/~wccc99/; WCCC99 – 9th World Computer Chess Championship – WCCC 99 in Paderborn.